Dasar-dasar analisis spektral

Analisis spektral merupakan salah satu aplikasi pengolahan sinyal, tujuan dari analisis spektral adalah untuk mengetahui frekuensi yang dikandung dari sinyal.

Pada posting ini saya mengawali dengan membuat Transformasi Fourier untuk menganalisa data pengukuran berupa data diskrit. salah satu Dasar-dasar spectral analysis adalah menggunakan Discrete Fourier Transform (DFT) yang berfungsi mentransformasi sinyal domain waktu ke domain frekuensi atau sebaliknya. secara lengkap teori tenteng DFT bisa dilihat di Wikipedia.org

Berikut adalah contoh Class untuk DFT dengan menggunakan bahasa pemrograman Delphi

TOMCOnstituent=class(TObject)
private
  FData:TList;
  FAmp:TList;
  nconst:integer;
  min,max:extended;
  VMin,VMax:extended;
  numFreq:integer;
  function AddConst(a,b:extended):integer;
  procedure ChangeAmp(index:integer;a,b:extended);
  function Counting:integer;
  function GetAmp(index:integer):TOMAmp;
  function GetData(Index:Integer):TOMData;
protected
public
  constructor Create;
  destructor Destroy;override;
  function AddData(waktu,elev:real):integer;
  procedure CurveFitting(M:integer);
  function Recalculate(waktu:extended):extended;
  function ExtractFreq:TArrayFloat;
  function ExtractAmp:TArrayFloat;
  function ExtractPhase:TArrayFloat;
  function ExtractConstituent:TArrayFloat;
  function showformula(decimal:byte):string;
  property Items[Aindex:integer]:TOMData read GetData;default;
published
  property Count:integer read Counting;
  property Freq_Num:integer read Counting;
  property Max_Value:extended read VMax;
  property Min_Value:extended read VMin;
end;

Sebagai contoh buatlah row data fungsi trigonometri dengan frekuensi 0.5 dengan amplitud dan fasa yang bervasiasi, misal: f(x) = 2*cos(0.5*t+1.5) dan f(x) = 5*cos(0.5*t-0.8) maka hasilnya akan sama seperti gambar di bawah (horizontal : frekuensi dan Vertikal : Amplitud), lihat bahwa puncak dari grafik tersebut pada frekuensi sekitar 0.5 :

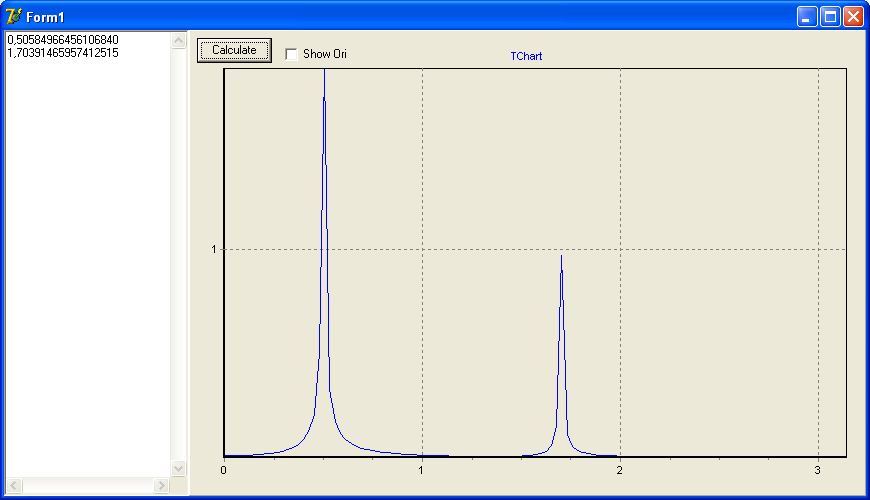
contoh lain bila menggunakan 2 frekuensi yang berbeda, misal : f(x)=2*cos(0.5*t+1.5)+1*cos(1.7*t+0.5) dan hasilnya seperti gambar berikut :

Contoh script tersebut dapat di di download di sini.